Od bitov h kubitom

O malokateri temi kroži toliko netočnosti, dezinformacij in nerealnih pričakovanj kakor o kvantnih računalnikih. Že dvajset let poslušamo, da bodo vsak hip v velikem slogu zavzeli trg in klasične računalnike postavili na smetišče zgodovine, saj bodo eksponentno hitrejši, tako da bo razbijanje danes nezlomljivih šifer mala malica. V vsem tem je zrno resnice, a ob zdravi meri skepse in z nekaj znanja.

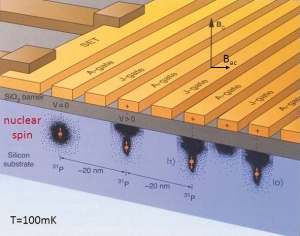
Na Univerzi v Novem Južnem Walesu so kubite izvedli s fosforjevimi atomi v silicijevem kristalu. Njihovo stanje krmilimo s tranzistorji prek vrat A, podatke med njimi pa prenašamo s tranzistorji prek vrat J.

O kvantnih računalnikih so prvikrat začeli razmišljati v 70. letih prejšnjega stoletja, ko so se s tem teoretično ukvarjali predvsem Rusi. Silovit teoretični razvoj je sledil v 80. letih, ko se je razvilo teoretično ogrodje, ki velja še danes. Leta 1985 je David Deutsch pokazal, kakšen bi moral biti splošen kvantni računalnik; to je kvantna ustreznica Turingovega stroja v klasičnem računalništvu. V 90. letih se je nadaljeval razvoj kvantnih algoritmov, videli pa smo tudi prve okorne praktične izvedbe kvantnih transformacij. V tem tisočletju se je razvoj preusmeril k praktični izvedbi kvantnih računalnikov, ki bodo zmogli izvesti vse elegantne teoretične zamisli. In to ni tako enostavno, kakor bi si mislili.

Čudni svet kvantov

Preden planemo k delovanju kvantnih računalnikov, moramo povedati nekaj nujnih osnov o kvantnih fiziki.

Imejmo pregrado z dvema režama. Če skoznjo posvetimo s svetlobo, na zaslonu za režo vidimo značilen interferenčni vzorec. Svetlobni valovi se med seboj ojačijo ali oslabijo, odvisno od faze. Z elektroni je enako: obnašajo se kot valovanje. Še bolj nenavadno postane vse skupaj, če pred reži namestimo detektor za elektrone. V tem primeru interferenčni vzorec izgine in elektroni se obnašajo kakor delci. Vsi objekti se vedejo kakor valovanje in delci, le da za velike objekte tega ne moremo opaziti.

Drugo spoznanje, ki bo pomembno vplivalo na kvantno računalništvo, pa je kolaps valovne funkcije. Meritev kvantnega sistema nujno povzroči spremembo merjene količine, s tem ko sistem prisili, da si jo izbere. Pred meritvijo je bil namreč sistem v superpoziciji vseh stanj hkrati. Šele z meritvijo smo ugotovili, kje je potoval elektron.

Delca sta lahko kvantno prepletena. Poenostavljeno rečeno, sta kvantno prepletena, če sta njuni stanji povezani. Potem z meritvijo stanja enega delca pridobimo informacijo o stanju drugega delca, čeprav je ta daleč stran. Delec pred meritvijo ni imel merjenega stanja; šele meritev ga je prisilila v izbiro. Hkrati pa je s tem meritev vsilila tudi drugemu delcu, da izbere ustrezno stanje.

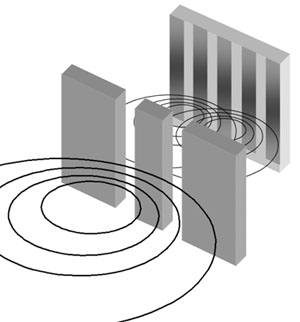
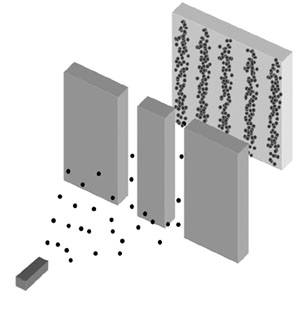
Pri prehodu valovanja skozi vzporedni reži na zaslonu vidimo interferenčni vzorec, pri prehodu delcev pa ne. Na kvantni ravni se vsi predmeti obnašajo dualistično – kot delci in valovanje hkrati. Če ne merimo, skozi katero režo potuje delec, vidimo interferenčni vzorec. Če pred eno izmed rež postavimo detektor, interferenčni vzorec izgine.

Kubiti

Osnovna enota informacije je bit in klasični računalniki manipulirajo z biti. Bit ima lahko vrednost 0 ali 1. Kvantni računalniki pa obdelujejo kvantne bite ali kubite. Bistvena razlika je omenjena superpozicija. Kubit obstaja v superpoziciji stanj 0 in 1, česar si klasično ne moremo predstavljati. To ne pomeni, da je kubit nekaj časa enak 0, potem pa 1, niti da je njegova vrednost nekje vmes. Superpozicijo razumemo tako, da je vrednost kubita 0 in 1 hkrati.

Superpozicija stanj nam zelo pomaga pri računanju. Vse operacije se namreč izvajajo na kubitih v superpoziciji vseh mogočih stanj, zato sistem računa vse možne kombinacije hkrati. Sliši se izvrstno, a fizike ne morete premagati. Kubiti so resda lahko v poljubni superpoziciji stanj, a s pomembno omejitvijo. Z meritvijo ne moremo (problem ni v znanju, temveč je to fizikalno nemogoče) pridobiti podatka o amplitudi stanj. Meritev nam vrne samo eno izmed stanj, v katerih superpoziciji je sistem kubitov. Katero stanje bomo izmerili, je popolnoma naključno in nemogoče napovedati; vemo le, da bo verjetnost zanj sorazmerna s kvadratom amplitude. V resnici je še huje: meritev je proces, ki uniči superpozicijo in kubit potisne v klasično stanje.

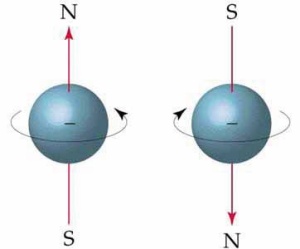
Spin je kvantna lastnost delcev, ki se pozna na magnetnem polju, kakor da bi ga povzročalo vrtenje nabitega delca. V resnici se ne vrti, saj imajo spin tudi nevtralni delci.

K sreči to ne izniči prednosti kvantnih računalnikov, saj je mogoče kvantne algoritme oblikovati tako, da so vse druge amplitude, razen tiste, ki nas zanima, zelo blizu nič. Če potem kvantni izračun ponovimo večkrat in dobimo vedno enak rezultat, smo lahko prepričani, da je to iskana rešitev. Ponavadi kvantne računalnike uporabljamo za probleme, ki jih je zelo težko rešiti, a je pravilnost dobljene rešitve mogoče nadvse enostavno preveriti (recimo faktorizacija velikih števil, iskanje po zbirki podatkov itd.).

Kvantni računalniki niso zmogljivejši, ker bi hitreje opravljali operacije nad biti, temveč ker lahko na njih poganjamo kvantne algoritme, ki isti izračun opravijo v bistveno manj korakih (v nižji časovni zahtevnosti).

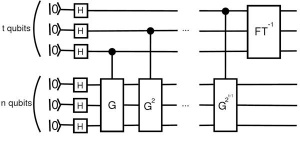
Shema dela kvantnega vezja, ki se uporablja v kvantnem algoritmu.

Težki in pretežki problemi

Kvantni računalniki ne bodo vsemogočni. Čeprav se je marsikateri ugledni reviji zapisalo, da bodo zmogli v polinomskem času (to pomeni zadovoljivo hitro) reševati NP-polne probleme, to ne drži. Pomembne so tri vrste problemov.

P-probleme lahko rešimo v polinomskem času, torej so jih tudi klasični računalniki sposobni rešiti. Takšna primera sta povezovanje grafov ali preverjanje praštevilskosti nekega števila.

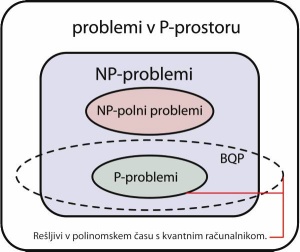
P-problemi so rešljivi v polinomskem času. NP-problemi niso rešljivi v polinomskem času, so pa rešitve preverljive v polinomskem času. NP-polni problemi so posebna vrsta problemov, ki bi bili vsi rešljivi z istim algoritmom v polinomskem času, če ta sploh je (ni znano). Množica BQP označuje probleme, ki jih kvantni računalniki lahko rešijo v polinomskem času. Vsi ti problemi so v P-prostoru, ker za rešitev potreba po pomnilniku narašča polinomsko s težavnostjo, čas pa seveda ne nujno.

NP-problemi za rešitev terjajo število korakov, ki raste eksponentno z dolžino problema,  rešitev pa lahko preverimo hitro – recimo iskanje deliteljev nekega števila. To znajo kvantni računalniki početi hitreje, a to še vedno niso NP-polni problemi.

NP-polni problemi so vrsta problemov, ki so spet rešljivi šele v eksponentnem času, a so si tako podobni, da bi rešitev enega pomenila rešitev vseh drugih. Taki so barvanje neme karte, potujoči trgovec, sudoku itn. Ni še dokazano, da zanje ni algoritma, ki bi jih rešil učinkovito, tj. v polinomskem času. Domneva se, da takšnega algoritma ni. Tisti, ki mu bo to ali nasprotno uspelo dokazati, bo dobil milijon dolarjev nagrade od ameriškega Clay Math Instituta. Teh problemov kvantni računalniki ne bodo reševali skoraj nič hitreje od navadnih računalnikov.

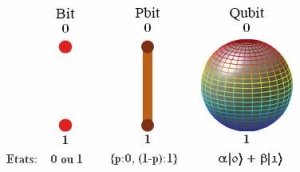
Klasični biti so lahko v stanju 0 ali 1. Kubiti niso z neko verjetnostjo v stanju 0 ali 1 – to bi bili verjetnosti biti ali pbiti (probability bits). Kubiti so v obeh stanjih hkrati.

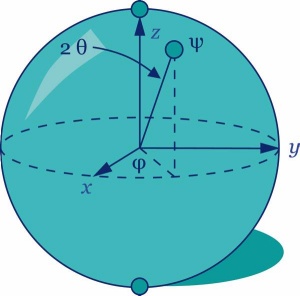
Na Blochovi krogelni lupini predstavimo superpozicijo stanj 0 (gor) in 1 (dol) kubita kot vektor, ki kaže iz središča sfere na površino, kjer sta azimutni in polarni povezana z amplitudama superponiranega stanja.

Kopiranje prepovedano

Kvantni sistemi so zanimivi, ker z njimi lahko počnemo stvari, ki jih z navadnimi računalniki ne moremo, obenem pa ne moremo početi nekaterih zelo trivialnih reči.

Navadne bite lahko kopiramo oziroma kloniramo, kubitov pa ne moremo. Razmislek pokaže, da je to pravzaprav edina možnost. Z branjem lahko pridobimo le eno izmed stanj, v katerih superpoziciji je kubit. Če bi kubite lahko klonirali, bi lahko to omejitev obšli, saj bi lahko kubit poljubno mnogokrat klonirali in potem prebrali njegovo vrednost. Fizika nam takšnega goljufanja ne dovoli.

Še bolj zanimivo pa je, da lahko kubite teleportiramo. Če oddajniku in sprejemniku pošljemo kvantno prepleten par kubitov, lahko na enem izmed kubitov para in na kubitu za teleport izvedemo ustrezno transformacijo in izmerimo stanje. Rezultat pošljemo z dvema klasičnima bitoma prejemniku, ki lahko z ustreznimi transformacijami obnovi teleportiran kubit. S tem nismo prekršili prepovedi kloniranja, saj smo z meritvijo nepopravljivo uničili superpozicijo stanja teleportiranega kubita pri oddajniku.

Nasprotna operacija od teleportiranja pa je prenos dveh bitov informacije z enim kubitom. Oddajnik prejme dva klasična bita informacije, ki ju mora prenesti k prejemniku. Na podlagi tabele, ki sta si jo predhodno izmenjala, glede na informacijo v bitih izbere ustrezno transformacijo in jo izvede na enem kubitu. Ko na drugem kubitu prejemnik informacije izvede druge transformacije, lahko iz rezultatov meritev sklepa, katero število (od 0 do 3) je poslal prejemnik. Z enim kubitom zaradi superpozicije stanj prenesemo dva klasična bita informacije.

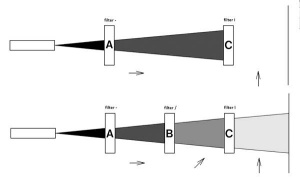
Vodoravno usmerjen filter A prepušča le vodoravno polarizirane fotone. Filter C, ki je usmerjen navpično, jih v celoti zadrži, ker je nanj pravokoten. Če pa med filtra postavimo poševno usmerjen filter, ki nanju ni pravokoten, bo ta prepustil del vodoravno polariziranih fotonov, ki se jim bo ob tem spremenila polarizacija v poševno. Navpični filter bo potem spet prepustil del teh fotonov. Dodajanje filtra v sistem torej poveča prepustnost. To izkoriščamo pri kvantnem varnem prenosu ključev.

Kvantni algoritmi

Na kvantnih računalnikih lahko poganjamo iste algoritme kakor na klasičnih, a ni prav nobenega razloga, da bi to počeli. Izvajajo jih počasneje od klasičnih, poleg tega jih pesti dekoherenca (vsaka interakcija od zunaj nepovratno uniči kvantno superpozicijo stanj,  tudi meritve). Zato imajo kvantni računalniki specializirane namene, v vsakdanjem življenju pa resne pomanjkljivosti. Kvantni računalniki ne bodo omogočili hitrejšega poganjanja iger v visoki ločljivosti.

Značilen zgled, kaj pa lahko storijo hitreje, je faktorizacija velikih števil. Ameriški matematik Peter Shor je leta 1994 odkril kvantni algoritem, ki faktorizira števila v polinomskem času, medtem ko je najhitrejši klasični algoritem eksponenten. Genialnost Shorovega algoritma je način, kako lahko z meritvijo kljub omejitvam dobimo uporaben podatek. Čeprav meritev vrne le eno izmed stanj, algoritem poskrbi, da imajo le uporabna stanja amplitude, ki so za praktične potrebe znatno različne od nič. Zato vedno preberemo rezultat. Prav tako je faktorizacija problem, ki ga je težko rešiti, a je rešitev mogoče enostavno preveriti.

Drugi zelo zanimiv algoritem je kvantno iskanje. Da bi na neurejenem seznamu s 10.000 vnosi našli pravega, mora klasični algoritem v povprečju izvesti 5.000 poizvedb. Poznamo pa Groverjev kvantni algoritem, ki jih mora v povprečju opraviti le 100. Pohitritev v nasprotju s Shorovim algoritmom tu ni eksponentna, temveč kvadratna.

Kvantni računalniki imajo tudi potencial za kvantne simulacije obnašanja molekul. Reševanje Schrödingerjeve enačbe je na klasičnih računalnikih kljub približkom zelo počasno; kvantni računalnik bo omogočil simulacijo v doglednem času.

Iz teorije v prakso

Postavimo zdaj visokoleteče algoritme na trdna tla. Dosedanje razglabljanje je bilo namenjeno kvantnemu programerju, ki ga ne zanima, kako kvantne sisteme postavimo v praksi – tako kot tudi za klasično programiranje ni treba poznati zgradbe tranzistorja. Kljub temu mora tranzistor nekdo izdelati in jih več skupaj zložiti v čip.

Kako torej narediti kubit in kako mu izmeriti stanje? Možnosti je več. Za kvantni računalnik morate izpolniti štiri DiVicenzove pogoje: potrebujete robustne kubite, univerzalni nabor vrat, zanesljiv vhodni register n ­kubitov in ustrezne meritve.

Trenutno poznamo štiri glavne pristope k izvedbi kvantnega računalnika: kvantno optiko, hladne atome, spinski in superprevodni. Njihov razvoj še vedno poteka, saj jim pri vseh sploh še ni uspelo izvesti vseh teoretičnih kvantnih vrat.

Pri kvantni optiki (ali kvantni elektrodinamiki) potrebujemo nevtralne atome in fotone, ki jih lahko uporabimo na dva načina. Bodisi so atomi nosilci kvantne informacije in fotoni poskrbijo za povezavo med njimi (prepletenost) bodisi je nasprotno. Vse skupaj se mora dogajati v elektromagnetnem polju.

Hladni atomi so ohlajeni na vsega nekaj mikrokelvinov, kjer postane njihova kvantna narava pomembna. Ultrahladni atomi se lahko vedejo kot kvantni računalnik, če jih posadimo na optično rešetko (tako imenujemo interferenco več izvirov laserske svetlobe). Druga možnost je, da ultrahladne atome pretvorimo v ione z izbijanjem elektronov in ujamemo v elektromagnetnem polju. To je ena izmed najbolj obetavnih metod, saj so tako že pripravili sistem 14 kvantno prepletenih ionov, prav tako so že praktično izvedli vrata CNOT.

Jedrska magnetna resonanca ali NMR (to gotovo poznate kot metodo za slikanje mehkih tkiv) za kubite uporablja spin molekul. Ta tehnika je manj uporabna od drugih, ker pri NMR kot sistem deluje celoten ansambel molekul, kar prinaša velik šum. IBMu je sicer uspelo demonstrirati delovanje Shorovega algoritma na 7-kubitnem kvantnem računalniku z metodo NMR, a kakšnega večjega napredka v zadnjih desetih letih ni bilo. Za občutek: IBMu je tako uspelo ugotoviti, da sta delitelja števila 15 tri in pet.

Superprevodnost pa je lastnost nekaterih materialov, da pri dovolj nizki temperaturi izgubijo vsakršno električno upornost. To prinaša številne zanimive posledice, med katerimi je za kvantne računalnike najpomembnejši Josephsonov učinek. Če med dva kosa superprevodnika vstavimo izolator, bo skozi tak člen, ki ga imenujemo Josephsonov stik, tok kljub temu tekel brez izgub. To je sila čudno, a matematično izpeljano in fizikalno dokazano, v kvantnem svetu pa prostora za čudenje že zdavnaj ni več. Če izdelamo prstan iz superprevodnika z več Josephsonovimi stiki, smo dobili osnovno enoto za kvantni superračunalnik.

Prototip kvantnega računalnika v Googlovem laboratoriju

Zdaj pa zares!

Najbliže kvantnemu računalniku so prišli v kanadskem podjetju D-Wave, ki so v sodelovanju z Naso in Googlom izdelali D-Wave Two. Oglašujejo ga kot adiabatni kvantni računalnik (beseda adiabatni tu nima klasičnega termodinamičnega pomena »brez izmenjave toplote«). Izkorišča adiabatni izrek, da fizikalni sistem ostane v trenutnem lastnem stanju, če je motnja zadosti počasna in če je energijska vrzel dovolj velika.

Poenostavljeno povedano, so adiabatni kvantni računalniki nekoliko drugačni od šolskih sistemov, ki smo jih teoretično opisali na začetku. Vzemite to kot razliko med idealnim Carnotovim toplotnim strojem in dejanskim dizelskim motorjem, ki poganja vaš avtomobil. V detajlih in izvedbi sta različna, načeloma pa gre v obeh primeri za toplotni stroj.

Tako je tudi z D-Wave Two. Ker gre za adiabatni kvantni računalnik, si lahko privošči nekoliko slabšo kvantno prepletenost in več šuma, pa še vedno deluje. Prav tako je tudi odpornejši za kvantno dekoherenco zaradi delovanja okolice, saj je kvantni sistem v osnovnem stanju in niže ne more, okolica pa je dovolj ohlajena, da je termična energija manjša od vrzeli med osnovnim stanjem kvantnega sistema in prvim višjim stanjem. Možnost za fluktuacije je tako manjša.

Komercialni kvantni računalnik D-Wave Two sta kupila tudi NASA in Google.

Takoj po njegovi predstavitvi so se vnele žolčne razprave, ali gre dejansko za kvantni računalnik ali ne. Dejstva govorijo v obe smeri. Da gre za kvantni računalnik, kaže že zanimanje Googla in Nase. Trdnejši dokaz so posredovali iz D-Wava, saj so na svojem računalniku rešili Ramseyjev problem za nekatere znane vrednosti in ugotovili, da najde rešitve bistveno hitreje od klasičnega računalnika. Če k temu dodamo še zapleteno zgradbo in na skoraj absolutno ničlo ohlajen centralni računski del, se zdijo dokazi precej prepričljivi. Pravijo, da sistem tudi sicer izkazuje obnašanje, ki ga ni mogoče opisati nekvantno. Adiabatno kvantno računalništvo je tako novo področje, da o njem niso prepričani niti, ali resnično potrebuje kvantno prepletenost. Dvome poraja predvsem skrivnostnost, saj D-Wave noče razkriti vseh podrobnosti o računalniku. Zagotovo vemo, da gre za 512-bitni računalnik. Lockheed Martin mu verjame, saj so leta 2011 kupili en primerek za 10 milijonov dolarjev. Videli bomo že kmalu, saj za leto 2015 napovedujejo D-Wave Three, ki naj bi bil sposoben izračunati Ramseyjeva števila za koeficiente, ki jih s klasičnimi računalniki ne moremo.

D-Wave Two seveda ni edina praktična implementacija kvantnega računalnika, le prva komercialna je.

Zgodovina kvantnega računalništva

1973 – Alexander Holevo pokaže, da iz n kubitov ne moremo pridobiti več kot n klasičnih bitov informacije (Holevov izrek).

1980 – Juri Manin predlaga kvantno računalništvo.

1981 – Richard Feynman pokaže, da klasičen računalnik ne more učinkovito simulirati kvantnega sistema, zato predlaga kvantni računalnik.

1981 – Tommaso Toffoli odkrije reverzibilna Toffolijeva vrata.

1982 – Paul Benioff ponudi prvo rigorozno obravnavo kvantnih algoritmov.

1985 – David Deutsch opiše prvi univerzalni kvantni računalnik, podobno kot je Turing opisal univerzalni klasični računalnik.

1991 – Artur Erkert pokaže, kako uporabiti kvantno prepletenost za varno komunikacijo.

1994 – Peter Shor odkrije kvantni algoritem za faktorizacijo števil.

1994 – Ignacio Cirac in Peter Zoller predlagata eksperimentalno izvedbo kvantnih vrat.

1995 – Shor in Andrew Steane pokažeta prve mehanizme za kvantno odpravljanje napak.

1995 – Prva eksperimentalno izvedba kvantnih vrat: CNOT vrata z ujetimi ioni.

1996 – Lov Grover odkrije kvantni algoritem za iskanje v neurejeni bazi.

1996 – David DiVincenzo postavi seznam zahtev, ki jih mora izpolnjevati vsak eksperimentalni kvantni računalnik.

1998 – Prva eksperimentalna izvedba kvantnega algoritma.

1998 – Prvi delujoč 3-kubitni kvantni računalnik na NMR.

2000 – Prvi delujoč 5-kubitni kvantni računalnik.

2000 – Prvi delujoč 7-kubitni kvantni računalnik.

2000 – Adiabatni kvantni računalniki prvič omenjeni kot nov model za kvantne izračune.

2001 – Prva praktična izvedba Shorovega algoritma: IBM in Stanford sta ugotovila, da tri in pet delita 15.

2005 – Prvi delujoč kvantni bajt – kubajt.

2006 – Prvi delujoč 12-kubitni kvantni računalnik.

2008 – D-Wave izdela prvi delujoč primerek 128-kubitnega kvantnega računalnika.

2011 – D-Wave pokaže komercialni 128-kubitni računalnik D-Wave One.

2013 – D-Wave izda 512-kubitni računalnik D-Wave Two.

Okrepljeni so teoretični dosežki, neokrepljeni so eksperimentalni dosežki,

Kam vse to vodi?

Prihodnost bo še zelo zanimiva. Kvantni računalniki so trenutno še v povojih. Z njimi lahko izračunamo to, kar znamo in zmoremo tudi s klasičnimi računalniki. A tako je z vsako novo tehnologijo. Ko bodo zaživeli v polnem sijaju, kar se bo gotovo zgodilo še v tem stoletju, bo človeštvo dobilo nesluteno računsko moč. Najprej bodo res padli nekateri danes nezlomljivi šifrirni algoritmi, a bomo poiskali nove. Problem bo le z danes zakodiranimi podatki, za katere si bomo tudi tedaj želeli, da bi ostali tajni. Sicer pa bodo kvantni računalniki omogočili simulacije, o katerih lahko danes le teoretiziramo. Tak zgled so simulacije prileganja molekul na tarčno mesto biomakromolekul, kar je nadvse uporabno pri iskanju zdravil. Danes je to zelo potraten postopek, ki obsega požrešne računalniške simulacije in dolga testiranja, v prihodnosti pa bodo kvantni računalniki to lahko mimogrede pogledali. Vojska bo z njimi verjetno poizkusila simulirati posledice jedrskih detonacij ali fuzijskih bomb, miroljubni znanstveniki pa bodo dobili orodje za študij fuzije in drugih novih potencialnih energetskih virov.

Ustanovitelj D-Wava Geordie Rose kaže kvantni računalnik. Kvantni del je v spodnjem čipu (pred napisom na lestvi).

Hladilni sistem v D-Wave Two.

Toda kot smo že pokazali, vsakdanjih dejavnosti kvantni računalniki ne bodo izvajali hitreje. Igranje iger, brskanje po spletu, pisanje besedila, zaganjanje računalnika bodo ostali enako počasni. Tudi nekaterih težkih matematičnih problemov zelo verjetno ne bodo reševali nič hitreje.

Po trenutnem poznavanju fizike so kvantni računalniki konec možnega razvoja. Dlje z doslej odkritim ne gre in če bomo želeli kdaj v prihodnosti izdelati fundamentalno zmogljivejše računalnike, bomo potrebovali nadgradnjo trenutne fizike. Ker sedanja fizika še ni zadovoljivo razložila gravitacije in poenotila vseh teorij, upanje ostaja.

 Toda brez pretiravanja lahko rečemo, da bodo kvantni računalniki prinesli revolucijo, ki bo primerljiva s tisto, ki so jo prinesli klasični računalniki v analogni svet. Upajmo le, da bomo še med živimi, ko se bo to zgodilo.